Колорирование 2 цвета: Актуальные способы окраски волос в два цвета: виды, инструкция, советы

Техника окрашивания волос в два цвета

Женщины любят меняться, привнося в свой имидж новые интересные детали. Обычное однотонное окрашивание уже давно не привлекает представительниц прекрасного пола.

Парикмахерское искусство ежегодно предлагает новые виды и техники. К ним можно отнести и колорирование, то есть окраску в два и более цвета.

Такой способ окраски позволяет добиться объема и фактурности, делает волосы более блестящими, а переливы цвета выразительными.

В фото галерее представлены варианты окрашивания волос в два цвета черный и белый, контрастный, на короткие и длинные локоны, для блондинок и брюнеток.

Содержание

• 1 Виды двухцветного колорирования
• 2 Окрашивание волос в два цвета с применением техники треугольника
• 3 Двухцветное окрашивание для блондинок
• 4 Двухцветное окрашивание для брюнеток

Виды двухцветного колорирования

Окрашивание в два цвета тоже бывает разным. Рассмотрим его основные виды.

• Брондирование
  

Здесь найден ответ в решении спора, кто же все-таки привлекательнее, блондинка или брюнетка. В основе окрашивания — светлый коричневый оттенок, который постепенно к кончикам плавно осветляется, создавая эффект выгоревших прядей.

Это помогает сделать незаметным переход от уже отросших корней волос к окрашенным, так что нет необходимости очень часто посещать салон красоты. Для брондирования недопустим резкий контраст цветов, его особенность заключается именно в придании максимальной естественности прическе.

• Омбре (другими словами деграде) 

Это поперечное колорирование, представляет собой окрашивание двумя цветами по горизонтали, то есть на корни наносится чаще всего более темный оттенок, а кончики окрашиваются в другой цвет. Зачастую для кончиков выбирается более светлый тон, но могут быть также использованы и яркие контрастные цвета.

Омбре стало очень популярным видом, сегодня многие звезды появляются именно с таким цветом волос.

• Классическое колорирование

Представляет собой продольное попеременное окрашивание прядей, помогающее добиться переливов и игры цвета. С помощью колорирования можно выделить несколько контрастных светлых прядей на темном фоне и обрамить ими овал лица, можно добиться эффекта бликования, для этого выбираются оттенки одной гаммы, один из которого светлее предыдущего на один тон.

Они наносятся по всей голове, при этом более светлые пряди чередуются с темными. Для колорирования могут быть использованы любые оттенки.

Окрашивание волос в два цвета с применением техники треугольника

Это очень интересный метод. Его суть заключается в выделении из общей массы волос треугольника и последующей его окраске другим цветом. Треугольник может быть равнобедренный, с тупым углом или прямоугольный. Все зависит от фантазии мастера. Пряди могут быть выбраны в зоне челки, а могут быть сбоку или сзади.

Интересным является контрастное окрашивание, когда, например, на основном фоне светлых волос выделяют треугольник и тонируют его каким-нибудь ярким цветом.

Треугольник может быть один, но допускается и применение несколько треугольников. Для этого используется фольга, которую загибают пополам горизонтально, а уголки заворачивают, чтобы она крепко держалась на голове.

Данную технику лучше применять для окрашивания прямых волос преимущественно средней длины. Лучше не использовать ее на кудрявых локонах. Эффект может не оправдать ожиданий.

Технику Омбре окрашивания в два цвета  смотрите на видео:

Двухцветное окрашивание для блондинок

Колорирование светлых волос сделать намного проще, чем темных. Для этого нет необходимости осветлять пряди, поэтому структура волос повреждается значительно меньше, а эффект просто поражает своей красотой и оригинальностью.

Чтобы добиться переливов цвета, достаточно высветлить некоторые пряди на несколько тонов, а оставшиеся покрасить в близкий цвет, не слишком контрастирующий со светлыми волосами. Так можно добиться эффекта выгоревших волос.

Для колорирования блондинки могут выбирать все оттенки каштанового, рыжего, красного и пепельного. В сочетании со светлыми волосами очень оригинально смотрится неординарный вариант, когда, например, на кончики наносятся яркие цвета: красный, фиолетовый, розовый, синий и другие.

Сегодня очень популярным является так называемое окрашивание «соль и перец», когда на голове сочетаются два пепельных оттенка. В итоге получается холодный цвет.

Двухцветное окрашивание для брюнеток

Чтобы получить желаемый результат, брюнеткам придется немного потерпеть. Если волосы слишком темные, то для начала их придется слегка высветлить, чтобы желаемый оттенок лег ровно и получился таким, каким его задумал мастер и клиент.

Конечно, это не пройдет для волос бесследно, зато на выходе получится шикарный результат. К тому же, сегодня существует столько средств для восстановления структуры волос, что их небольшое повреждение при выполнении процедуры не станет никакой проблемой. Если правильно ухаживать за волосами, они всегда будут иметь здоровый вид.

Для колорирования брюнеткам подойдут следующие оттенки:

• молочного шоколада,
• корицы,
• темной пшеницы
• и вся золотистая гамма цветов.

Также вместо продольного окрашивания можно применить ультрамодное поперечное и окрасить нижнюю часть волос в необычные оттенки красного, рыжего, золотистого или даже синего или изумрудного.

Можно также осветлить несколько прядей по всему периметру головы или затронуть пряди около лица или челку. Корни затрагивать не рекомендуется.

Не стоит забывать, что выбор цветов напрямую зависит от возраста и статуса женщины.

То, что допускает в своей внешности девушка в семнадцать лет, может быть не совсем уместно для бизнес-леди среднего возраста.

Окрашивание в два цвета — настоящий тренд сезона. С его помощью можно добиться абсолютно уникальной прически, которую вы точно не найдете у кого-либо еще.

Подобное окрашивание украшает, создает объем и придает блеск, позволяя освежить образ, не прибегая к традиционному однотонному окрашиванию всей головы. Колорирование позволит вам попробовать новые оттенки и поэкспериментировать с собственной внешностью.

Не бойтесь меняться, и вам всегда будет гарантировано отличное настроение!

Окрашивание волос в два цвета

Почему с новой прической начинается новый этап жизни, понять могут только женщины. Новые стильные стрижки, а иногда даже изменение цвета волос на пару тонов способны придать уверенности в себе. Окрашивание волос в два цвета – новая модная парикмахерская тенденция, к которой дамы начали обращаться все чаще. Два разных тона краски способны создать уникальный стильный имидж.

Преимущества покраски волос в два цвета

Окрашивание в два цвета – отличная идея для тех, кто хотел бы сменить имидж, но при этом не делать традиционного мелирования. Помимо того, что выглядит двойное окрашивание весьма неординарно, этот тип покраски может похвастаться и другими преимуществами:

1. При правильно подобранных тонах краски будет создаваться визуальный эффект объема. Волосы будут казаться более густыми и пышными.
2. В отличие от традиционного окрашивания и большинства видов мелирования покраска двумя цветами совершенно неприхотлива и не требует частых корректировок.
3. Необычная окраска волос в два цвета привлекает внимание окружающих. Таким образом, волосы перенимают на себя все взгляды и отвлекают от всех недостатков кожи (если таковые, конечно, имеются).
4. Такой метод окраски считается более лояльным, в особенности, если на части прядей будет сохраняться натуральный цвет волос.
5. Неоспоримый плюс – универсальность. Двойное окрашивание подходит обладательницам всех типов волос. Главное – подобрать подходящие оттенки краски.

Виды окрашивания волос в два цвета

Разновидностей двухцветного окрашивания волос существует достаточно много, поэтому подобрать что-то интересное для себя смогут даже самые привередливые модницы:

1. Поперечное колорирование принято называть также балаяжем или деграде. Заключается этот метод в использовании двух разных оттенков одного цвета. При покраске волос в два цвета методом поперечного колорирования прокрашивать пряди нужно полностью от корней до кончиков. Чередуйте разные оттенки краски. Результат окрашивания выглядит натуральным и в то же время необычным.
2. Отлично выглядят волосы, окрашенные в два цвета, по методу омбре или горизонтального колорирования. Принцип покраски такой же, как и при поперечном колорировании – используются два оттенка одного цвета. Но прокрашиваются волосы не по всей длине, а начиная с середины локона. Главная особенность метода – в плавности перехода. Все должно выглядеть максимально естественно.
3. Один из самых сложных методов – 3D-окрашивание в два цвета. Сделать его в домашних условиях практически невозможно. Для покраски используются разные оттенки краски одной цветовой гаммы. В результате прическа выглядит пышной и объемной.
4. Мажимеш – один из самых лояльных методов окрашивания в два цвета, при котором выбирается краска для волос на кремовой основе с добавлением натурального воска.
5. Частичное колорирование позволяет акцентировать внимание на отдельном элементе прически. Лучше всего смотрится оно на ассиметричных стрижках. При желании можно выделить только одну прядку или челку.
6. Шатуш – метод, позволяющий добиться эффекта естественного выгорания. Красками светлых оттенков прокрашиваются отдельные прядки, за счет чего визуально увеличивается объем прически.

Прежде чем красить волосы в два цвета, следует подобрать самый подходящий метод окрашивания и оттенки краски:

1. Яркие цвета хорошо смотрятся на молодых девушках. Дамам же постарше лучше отдать предпочтение более натуральным тонам краски.
2. Контрастные цвета старят и визуально делают прическу менее объемной.
3. Окрашивание по технике омбре лучше смотрится на волнистых волосах.
4. Обладательницам смуглой кожи лучше отдать предпочтение мелированию.

 

Статьи по теме:

Пиксельное окрашивание волос Интересуетесь последними тенденциями в мире парикмахерского искусства. Тогда обязательно прочитайте нашу статью, которая посвящена пиксельному окрашиванию. Узнайте об особенностях этой технологии, нюансах ее выполнения, а при желании – попробуйте методику самостоятельно.	Французское мелирование Хотите освежить прическу к летнему сезону и придать волосам удивительный натуральный блеск, не повреждая их? Тогда обратите внимание на нашу статью. Материал посвящен французской разновидности блондирования, которая позволит бережно осветлить локоны.
Калифорнийское мелирование на темные волосы Калифорнийское мелирование – окрашивание, которое применяется совсем недавно, но за короткое время оно завоевало множество поклонниц. Читайте нашу статью о том, как мастерам удается добиться потрясающего эффекта темных полос у корней, и одновременно осветлить вертикальные пряди.	Мелирование на русые волосы Мелирование на русые волосы – это классика. Таким безобидным способом женщины изменяют свой образ, разбавляя его легкостью и игривостью. О том, какие виды мелирования существуют, и как правильно окрашивать светло-русые и темно-русые волосы, вы узнаете из нашей статьи.

 

5.8 Раскраска графика

Как мы кратко обсуждали в разделе 1.1, наиболее Знаменитая проблема раскраски графа — это, безусловно, проблема раскраски карты. предложенный в девятнадцатом веке и окончательно решенный в 1976 году.

Определение 5.8.1 Правильная раскраска графа — такое присвоение цветов вершинам графа, что никакие два соседние вершины имеют одинаковый цвет. $\квадрат$

Обычно мы опускаем слово «правильная», если только другие типы окраски не используются. также в стадии обсуждения. Конечно, «цвета» не обязательно должны быть актуальные цвета; они могут быть любыми различными метками — целыми числами, для пример. Если граф несвязен, каждая компонента связности может быть окрашены самостоятельно; если не указано иное, мы предполагаем, что графы подключены.

Мы также предполагаем, что графы в этом разделе простые.

Пример 5.8.2. Если вершины графа представляют академические классы, а две вершины смежны, если в соответствующих классах есть люди общий, то раскраска вершин может быть использована для планирования занятий встречи. Здесь цвета будут обозначать время расписания, например 8MWF, 9MWF, 11ТТ и др. $\квадрат$

Пример 5.8.3. Если вершины графа представляют радиостанции, а две вершины являются смежными, если станции расположены достаточно близко к мешают друг другу, можно использовать раскраску, чтобы назначить частоты, не создающие помех для станций. $\квадрат$

Пример 5.8.4. Если вершины графа представляют сигналы светофора в пересечение, и две вершины смежны, если соответствующие сигналы не могут быть зелеными одновременно, можно использовать окраску, чтобы обозначают наборы сигналов, которые могут быть зелеными одновременно. $\квадрат$

Определение 5.8.5. Множество $S$ вершин в графе является независимым, если никакие два вершины $S$ смежны. $\квадрат$

Если граф правильно раскрашен, вершины, которым присвоены определенный цвет образует независимый набор. Имея граф $G$, легко чтобы найти правильную раскраску: дайте каждой вершине различную цвет. Ясно, что интересное количество — это минимальное количество цвета, необходимые для раскрашивания. Также легко найти независимых наборы: просто выберите вершины, которые взаимно несмежны. Один набор вершин, например, является независимым и обычно находит большее независимые множества легко. Интересное количество — максимальный размер независимого множества.

Определение 5.8.6 Хроматическое число граф $G$ — минимальное количество цветов, необходимое для правильной раскраски; она обозначается $\chi(G)$. номер независимости от $G$ максимальный размер независимого множества; это обозначается $\alpha(G)$. $\квадрат$

Естественный первый вопрос об этих графические параметры является: насколько маленькими или большими они могут быть в графе $G$ с $n$ вершины.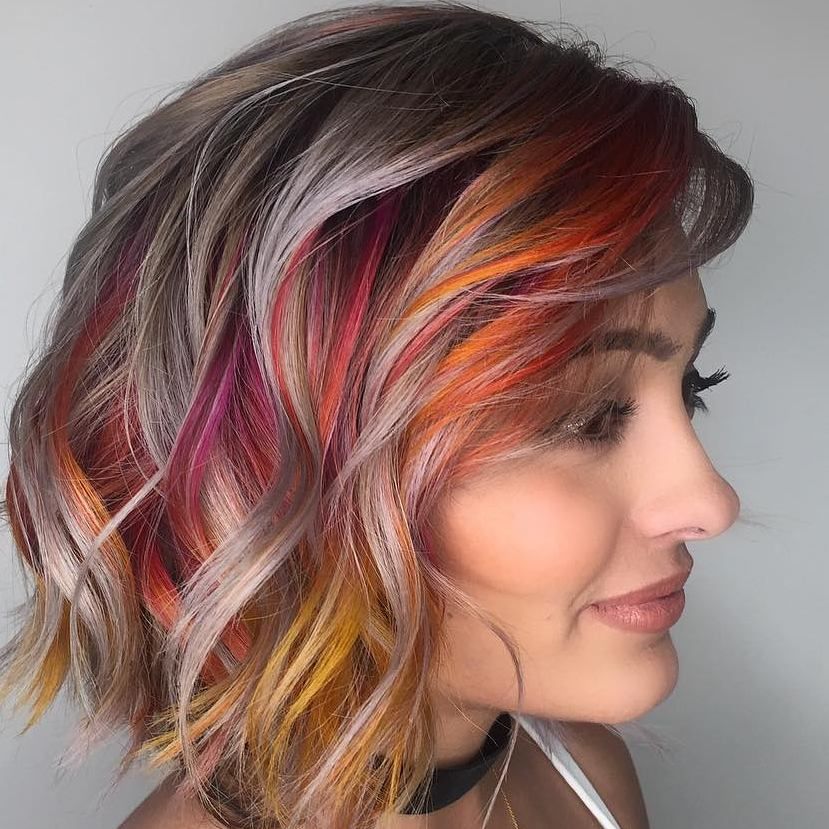 Легко видеть, что $$\выравнивание{ 1&\le \chi(G)\le n\cr 1&\le \alpha(G)\le n\cr }$$ и что все пределы достижимы: граф без ребер имеет хроматическое число 1 и число независимости $n$, а полный граф имеет хроматическое число $n$ и число независимости 1. Эти неравенства поэтому не очень интересны. Мы увидим некоторые, которые более интересный.

Другой естественный вопрос: какова связь между хроматическим номер графа $G$ и хроматический номер подграфа $G$? Это тоже просто, но иногда весьма полезно.

Доказательство. Любая раскраска $G$ обеспечивает правильную раскраску $H$ просто за счет присвоение тем же цветам вершинам $H$, что и в $G$. Это означает, что $H$ можно раскрасить в цвета $\chi(G)$, например еще меньше, чего мы и хотим. $\qed$

Часто этот факт интересен «наоборот». Например, если $G$ имеет подграф $H$, являющийся полным графом $K_m$, то $\chi(H)=m$ и, следовательно, $\chi(G)\ge m$. Подграф $G$, являющийся полным графом, называется клик , и есть соответствующий графический параметр.

Определение 5.8.8. кликовое число графа $G$ равно наибольшее $m$ такое, что $K_m$ является подграфом $G$. $\квадрат$

Заманчиво предположить, что только способов графа $G$ может потребоваться $m$ цветов при наличии такого подграфа. Это неверно; графы могут иметь высокое хроматическое число при низком кликовом числе; см. рисунок 5.8.1. Легко видеть, что это граф имеет $\chi\ge 3$, потому что в графе много 3-клик. график. В общем случае может быть трудно показать, что граф не может быть раскрашены заданным числом цветов, но в этом случае легко видим, что на самом деле граф нельзя раскрасить тремя цветами, потому что так много «вынуждено». Предположим, что граф можно раскрасить с помощью 3 цвета. Начиная слева если вершина $v_1$ получает цвет 1, тогда $v_2$ и $v_3$ должны быть окрашены в цвета 2 и 3, а вершина $v_4$ должен быть цвета 1. Продолжая, $v_{10}$ должен быть цвета 1, но это не допускается, поэтому $\chi>3$. С другой стороны, поскольку $v_{10}$ может быть цвет 4, мы видим $\chi=4$.

Пол Эрдёш показал в 1959 г., что существуют графы с произвольно большое хроматическое число и сколь угодно большой обхват (обхват это размер наименьшего цикла в график). Это гораздо сильнее, чем существование графов с высокой хроматическое число и низкое кликовое число.

Рисунок 5.8.1. Граф с кликой номер 3 и хроматическим числом 4.

Двудольные графы хотя бы с одним ребром имеют хроматическое число 2, так как две части являются независимыми наборами и могут быть окрашены с помощью один цвет. И наоборот, если граф можно раскрасить в 2 цвета, он двудольный, так как все ребра соединяют вершины разных цветов. Этот означает, что двудольные графы легко идентифицировать: раскрасьте любую вершину цвет 1; раскрасьте его соседей цветом 2; продолжая таким образом будет или не будет успешно раскрашивать весь график двумя цветами. Если оно терпит неудачу, граф не может быть двухцветным, так как все варианты вершин цвета принудительные. 9\чи |V_i| \ле \чи\альфа, $$ по желанию. $\qed$

Мы также можем улучшить верхнюю границу для $\chi(G)$. В любом графе $G$ $\Delta(G)$ — максимальное степень любой вершины.

Теорема 5.8.10. В любом графе $G$ $\ds \chi\le\Delta+1$.

Доказательство. Мы показываем что мы всегда можем раскрасить $G$ в цвета $\Delta+1$ с помощью простого жадный алгоритм : Выберите вершину $v_n$ и перечислите вершин $G$ как $v_1,v_2,\ldots,v_n$, так что если $i

Это, безусловно, верно для $v_1$. За 1 9 долларов0003

После того, как $v_1,\ldots,v_{n-1}$ были раскрашены, все соседи $v_n$ покрашены. были окрашены в цвета $1,2,\ldots,\Delta$, поэтому раскрасьте $\Delta+1$ может использоваться для окрашивания $v_n$. $\qed$

Обратите внимание, что если $\d(v_n)

Следствие 5.8.11. Если $G$ нерегулярно, то $\chi\le\Delta$. $\qed$

Существуют графы, для которых $\chi=\Delta+1$: любой цикл нечетной длины имеет $\Delta=2$ и $\chi=3$, а $K_n$ имеет $\Delta=n-1$ и $\чи=n$. Конечно, это обычные графики. Оказывается, это единственные примеры, т. е. если $G$ не является нечетным циклом или полным графом, то $\chi(G)\le\Delta(G)$.

Теорема 5.8.12. (теорема Брукса) Если $G$ — граф, отличный от $K_n$ или $C_{2n+1}$, $\chi\le\Delta$. $\qed$

Жадный алгоритм не всегда раскрашивает граф наименьшее возможное количество цветов. Рисунок 5.8.2 показывает график с хроматическим номером 3, но жадный алгоритм использует 4 цвета, если вершины упорядочены, как показано.

Рисунок 5.8.2. Жадная раскраска слева и наилучшая раскраска справа.

В общем случае вычислить $\chi(G)$ сложно, т. е. требуется большой объем вычислений, но есть простой алгоритм построения графа окраска не быстрая. Предположим, что $v$ и $w$ несмежны. вершины в $G$. Обозначим через $G+\{v,w\}=G+e$ граф, образованный добавлением ребро $e=\{v,w\}$ в $G$. Обозначим через $G/e$ граф, в котором $v$ и $w$ являются «идентифицированными», то есть $v$ и $w$ заменяются одним вершина $x$, смежная со всеми соседями $v$ и $w$. (Но учтите, что мы не вводите кратные ребра: если $u$ смежно и с $v$, и с $w$ в $G$, будет одно ребро от $x$ до $u$ в $G/e$.)

Рассмотрим правильную раскраску $G$, в которой $v$ и $w$ — разные цвета; то это также правильная раскраска $G+e$. Кроме того, любой правильная раскраска $G+e$ — это правильная раскраска $G$, в которой $v$ и $w$ имеют разные цвета. Таким образом, раскраска $G+e$ с наименьшим возможным количеством цветов есть наилучшая раскраска $G$, в которой $v$ и $w$ имеют разные цвета, то есть $\chi(G+e)$ — это наименьшее количество цветов, необходимое для раскрашивания $G$ так, чтобы $v$ и $w$ были разного цвета.

Если $G$ раскрашена правильно, а $v$ и $w$ одного цвета, то это дает правильную раскраску $G/e$, раскрашивая $x$ в $G/e$ с помощью тот же цвет, что и для $v$ и $w$ в $G$. Кроме того, если $G/e$ правильно окрашены, это дает правильную раскраску $G$, в которой $v$ и $w$ имеют того же цвета, а именно цвета $x$ в $G/e$. Таким образом, $\chi(G/e)$ это наименьшее количество цветов, необходимое для правильного окрашивания $G$ так, чтобы $v$ и $w$ одного цвета.

Итогом этих наблюдений является то, что $\ds\chi(G)=\min(\chi(G+e),\chi(G/e))$. Этот алгоритм можно применить рекурсивно, то есть если $G_1=G+e$ и $G_2=G/e$, то $\ds\chi(G_1)=\min(\chi(G_1+e),\chi(G_1/e))$ и $\ds\chi(G_2)=\min(\chi(G_2+e),\chi(G_2/e))$, где конечно ребро $e$ отличается на каждом графике. Продолжая таким образом, мы можем в конечном итоге вычислить $\chi(G)$ при условии, что в конечном итоге мы получим графы, которые «просто» раскрасить. Грубо говоря, поскольку $G/e$ имеет меньше вершин, а $G+e$ имеет больше ребер, мы должны в конце концов закончить построить полный граф по всем ветвям вычисление. Всякий раз, когда мы встречаем полный граф $K_m$, он имеет хроматическое число $m$, поэтому никаких дальнейших вычислений вдоль соответствующую ветку. Давайте сделаем это более точным.

Теорема 5.8.13 Приведенный выше алгоритм правильно вычисляет хроматическое число в конечное количество времени.

Доказательство. Предположим, что граф $G$ имеет $n$ вершин и $m$ ребер. Количество пар несмежных вершин равно $\na(G)={n\choose 2}-m$. Доказательство по индукции по $\na$.

Если $\na(G)=0$, то $G$ — полный граф и алгоритм немедленно прекращается.

Теперь заметим, что $\na(G+e)

Теперь, если $\na(G)>0$, $G$ не является полным графом, поэтому существуют несмежные вершины $v$ и $w$. По индукционному предположению алгоритм правильно вычисляет $\chi(G+e)$ и $\chi(G/e)$ и, наконец, вычисляет $\chi(G)$ из них за один дополнительный шаг. $\qed$

Хотя этот алгоритм очень неэффективен, он достаточно быстро, чтобы его можно было использовать на небольших графах с помощью компьютер.

Пример 5.8.14 Проиллюстрируем очень простым графиком:

Хроматическое число графика вверху равно $\мин(3,4)=3$. (Конечно, это довольно легко увидеть непосредственно.) $\квадрат$

Пример 5.8.1 Предположим, что $G$ имеет $n$ вершин и хроматическое число $к$. Докажите, что $G$ имеет не менее $k\choose2$ ребер.

Пример 5. 8.2 Найдите хроматическое число приведенного ниже графика, используя алгоритм в этом разделе. Нарисуйте все графы $G+e$ и $G/e$ сгенерированный алгоритмом в виде «древовидной структуры» с полным графики внизу, обозначьте каждый полный график его хроматическим число, затем распространите значения до исходного графика.

Пример 5.8.3 Покажите, что $\chi(G-v)$ есть либо $\chi(G)$, либо $\хи(G)-1$.

Пример 5.8.4 Докажите теорему 5.8.10. не предполагая каких-либо конкретных свойства порядка $v_1,\ldots,v_n$.

Пример 5.8.5 Докажите теорему 5.8.12 следующим образом. По следствию 5.8.11 нам нужно рассматривать только регулярные графики. Регулярные графы степени 2 просты, поэтому мы рассматриваем только регулярные графы степени не ниже 3.

Если $G$ не является 2-связным, покажите, что блоки $G$ могут быть окрашены с цветами $\Delta(G)$, и тогда раскраски можно изменить немного так, чтобы они вместе давали правильную окраску $G$.

Если $G$ 2-связен, покажите, что существуют вершины $u$, $v$, $w$ такие что $u$ смежно и с $v$, и с $w$, $v$ и $w$ не смежны. смежно, а $G-v-w$ связно. Учитывая такие вершины, цвет $v$ и $w$ с цветом 1, затем раскрасьте оставшиеся вершины жадным алгоритмом, подобным к этому в теорема \xrefnexternal{thm:почти ручьи}{cgt.pdf}, где $u$ играет роль $v_n$.

Чтобы показать существование $u$, $v$, $w$, как требуется, пусть $x$ будет вершина, не смежная со всеми остальными вершинами. Если $G-x$ 2-связен, пусть $v=x$, пусть $w$ находится на расстоянии 2 от $v$ (обоснуйте это), и пусть путь длины 2 равен $v,u,w$. Воспользуйтесь теоремой 5.7.4. чтобы показать, что $u$, $v$, $w$ обладают требуемыми свойствами.

Если $G-x$ не является 2-связным, пусть $u=x$ и пусть $v$ и $w$ равны (тщательно выбранные) вершины в двух разных концевых блоках $G-x$. Показывать что $u$, $v$, $w$ обладают требуемыми свойствами.

Брукс доказал теорему в 1941 году; это более простое доказательство связано с Ловаш, 1975 год.

4 шага, чтобы покрасить волосы в несколько цветов в домашних условиях

05 мая 2022 г.

К: Аланна Мартин Килкири | Makeup.com от L’Oréal

Поделиться этой страницей

Окрашивание волос в домашних условиях может быть сложной задачей, даже если вы просто переходите от одного цвета к другому. Если вы хотите покрасить волосы в несколько цветов, все становится еще сложнее. Но если вы будете следовать правильным шагам, это вполне возможно. Здесь Деб Розенберг, помощник вице-президента по образованию Redken, Matrix и Biolage, и Ник Стенсон, посол бренда Matrix, делятся своими лучшими советами по созданию разноцветных волос своими руками.

Что нужно знать перед началом работы

«Если вы ищете небольшое изменение или хотите сделать прическу темнее, нанесите краску от корней до кончиков», — говорит Розенберг. Но если вы хотите получить более яркий вид, нанесите краску на кончики волос перед корнями, чтобы цвет не выглядел неровным.

Если у вас окрашенные волосы, применение немного отличается. «Чтобы привести корни в соответствие с текущим оттенком окрашенных волос, просто нанесите краску на корни и протяните ее только в случае необходимости», — говорит Розенберг. Для яркого и стойкого цвета нам нравятся полуперманентные краски для волос от Good Dye Young.

The Process

«Если вам нужны забавные цвета или пастельные тона, обязательно осветлите волосы до нужного вам уровня осветления, а затем придайте волосам желаемый оттенок», — говорит Стенсон.